Wolfram Student Ambassadors: My Experience with Wolfram

Introduction
Whether it’s helping with my USAMTS problems or with that pesky Calc homework problem, Wolfram Alpha is pretty great. I mean, I remember plugging in this really complex two-variable system of equations, and it just solved it! Ok, as a mathematician, that could be counted as shortcutting, but I do this since it’s inproductive to just keep bashing at an unrealistic system of equations that you cannot solve. I’ll have a section on the exact problem below, but I think it’s pretty cool. As my appreaciaion for Wolfram increased, back in September I interviewed with Wolfram and became a part of the Wolfram Student Ambassadors program.
I just wanted to make this article pretty short, and I really just wanted to highlight some pretty cool things that you can do with Wolfram notebooks. Recently, on Wolfram Community, I posted this article that summarized my physics research and the cool properties of pendulums you can model with Wolfram. That article got me upgraded to a Featured Contributer, so I thought I’d talk a little about that here.
Mathematica
So Mathematica is Wolfram’s mathematical computation language that many professionals in STEM fields use. Unlike other systems, Mathematica applies intelligent automation in every part of the system, from algorithm selection to to plot layout and and user interface design.

Above, for my article I created a pendulum diagram with Mathematica and the code is pasted above with the pendulum below it. Of course, the code looks pretty intimidating, but actually a lot of Mathematica is just writing what you want in words. I’m exactly painting which line I want where or how high I want a certain circle. But otherwise, the implementation isn’t too advanced so it’s very beginner friendly.

Above is another example of a dense Mathematica block in my article. While it looks pretty intimdiating, for any of you who are familiar with advanced physics, I just rewrote a Euler Lagrange equation above! In essence, I wanted to graph the solutions to a Lagrangian motion equation and a regular graphing tool like Desmos would not be able to compute that so I turned to Mathematica.
If you want to check out my full article, you can find it here!
Wolfram Alpha
As a prize from placing in the USA Mathematical Talent Search (USAMTS) competition, I got a year-long subscription to Wolfram Alpha Pro and Mathematica. It’s pretty nice! At least with Wolfram Alpha, it tackles those pesky equations that I wouldn’t be able to solve by hand. Here’s a problem from Year 33 of USAMTS…

And there we go! Although, the equation that I plugged into above was after subsituting equation 1 into equation 2 it still gave us $\frac{1011}{1010}$ as the answer right away! I’m sure there’s a more elegant way to solve it, but this is a nice way to check our answers.
And currently I have Wolfram Premium which is nice because if I plug in a triple integral it’ll give me the steps to solve the problem so that I can understand it. If you are a math interested student, rather than buying Wolfram Premium, I encourage you to try out USAMTS!
Wolfram Player
I also just wanted to highlight Wolfram Player very quickly before I ended this article. I used Wolfram Player for my research project, and it’s a way to make animations or simulations with Wolfram language since other softwares cost money or take up a bunch of storage. Here’s a screenshot of some cool demonstrations down below. There’s a whole archive of them on Wolfram and they are all incredibly intricate.
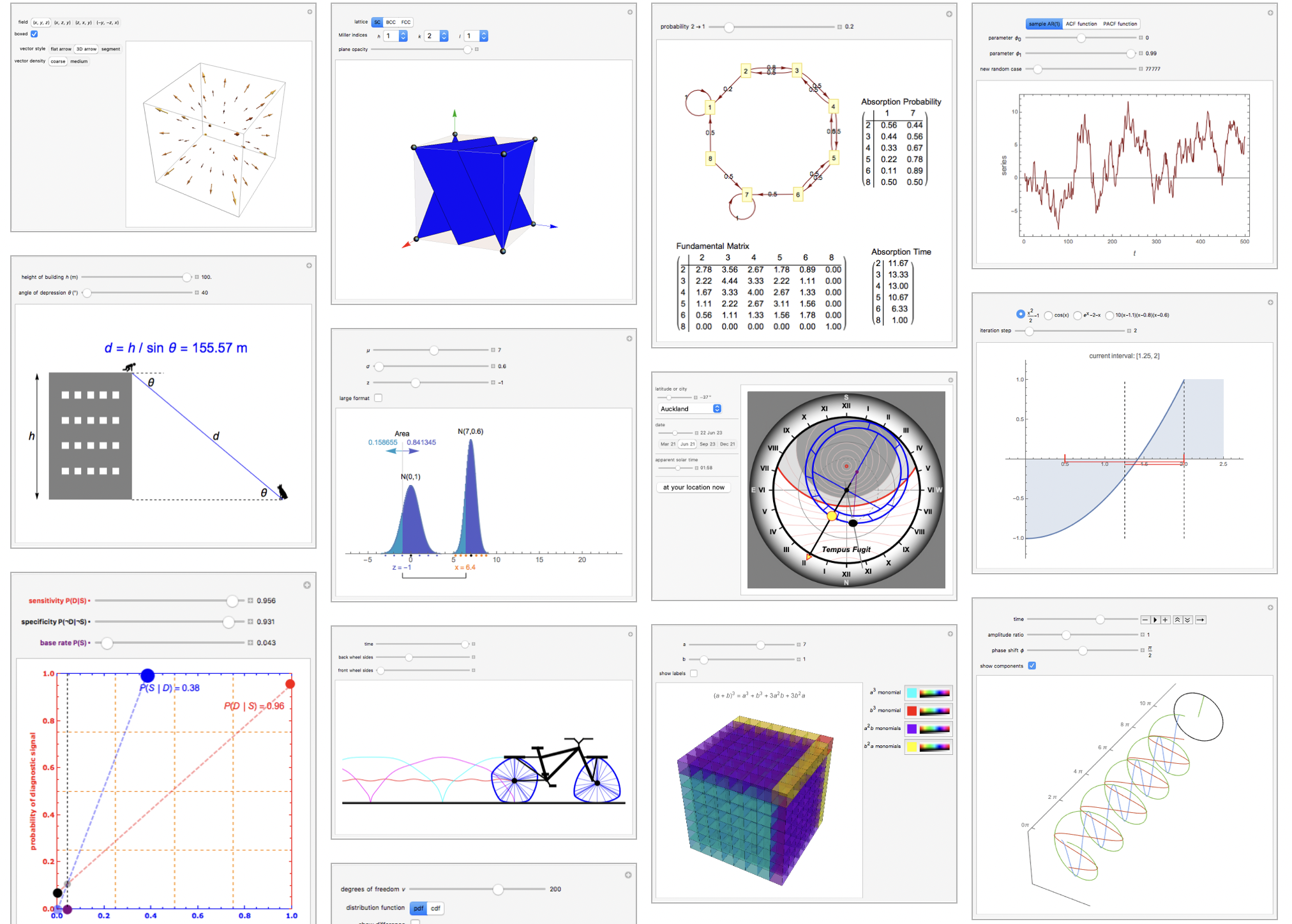
Conclusion
Overall, Wolfram is very cool and learning Mathematica, Wolfram Language, or any other Wolfram related languages will be incredibly helpful whether you are a student, researcher, or just anyone who’s interested in solving complex problems! Wolfram has a bunch of practice guides online so following any of those should be good enough to get a good sense of the language. Stay tuned for the next article.