Blaise Pascal: Well, there's the triangle.

Introduction

While I was doing some AMC and AIME problems, I encountered Pascal’s triangle endless times. It came up a lot in combinatorial problems, and it’s quite cool how theorems like the Hockey Stick Identity come from it. I also always thought mathematicians like Gauss had a interesting childhood, I mean he solved the $\frac{n(n+1))}{2}$ problem in Elementary School. So, was Pascal the same? Let’s find out…

Keep in mind that Pascal was alive during the 1600s, which was a time of the Great Awakening, so there is comparably more information on him than someone like Ptolemy. This time period was also a time where exploration amongst the European powers was in fashion, but since Pascal was mostly in France, they would deal with the Thirty Years War. So similarly, Pascal chose the exploration of mathematics.

Early Life

Blaise Pascal was born in Clemont, France in 1623 and he was a member of the aristocratic class. The Pascals had about $10 - 20 million dollars of wealth in today’s currency.

It’s safe to say that Blaise was a child prodigy. When he was younger, since he was part of the higher classes, he was easily exposed to Math and Science since he didn’t have any chores to do. They had a couple maids for that – sounds nice doesn’t it? His father recognized his talent and took him to the activites of high society, like intellectuals talking over a cup of tea. In fact, Pascal himself participated in these talks as a toddler to his pre teen years and was acknowledged by the famous philospher and mathematician Descartes.

It was at the bright age of 16 years old, that he wrote a treatise about a certain mathematical concept. It wasn’t just any treatise, but it was Pascal’s Theorem. It deals with Projective Geometry, so if you’re into that stuff, I talk about it later in the article.

One thing I find quite funny about his childhood is that when he was one years old, he was gravely sick. His parents chalked it up to the work of a witch – this was a little before the Salem witch trials. There was an old woman who was basically the babysitter for Pascal, so when he wasn’t getting better, his parents blamed the old woman. Shockingly, she confessed that she cast an evil spell on him which made him sick (This obviously isn’t true she must’ve felt very pressured). She then threw two cats out the window (they died, the poor cats!) and rubbed some leafy paste on his stomach. Well, he got better miraculously after that little ritual. But, we don’t know what happened to that lady.

This is foretelling of his ill health in his adult life. Many say that he was cursed, but maybe it’s just karma for killing those two cats.

Later

At the time it was popular for many young artistocrats to follow their father’s footsteps, and follow in their life work. So Pascal’s father was working as a tax supervisor, and the young mathematician would work on his projects and studies while occassionally helping his father. He saw that his father was working with calculators often and saw that it was incredibly tedious. He then began his 3 year project on a new calculator. MIT would’ve surely taken him, but that would be a severe downgrade.

But the real story is that during this time, around the 1630’s, France was fighting in the Thirty Years War (one of the most brutal wars in European history). France kept taking out government bonds, and this made Pascal’s family standing drop from aristocrat to a low middle class. Pascal’s father disagreed with the regional cardinal’s fiscal policies, so he fled France leaving his three children behind. Soon enough, his daughter, Jacequline, started to perform at childrens plays (with the cardinal in attendance) that the cardinal forgave his family. Pascal’s father was then reinstated as the regional tax collector, and had boatloads of work. Hence, Blaise Pascal’s invention.

This is Pascal's Mechanical Calculator, stored in the Conservatoire National de Art et Metiers, Paris.

He designed the project when he was 19 years old, but then he went on to create 50 prototypes till 1945 until he finally presented his findings. In fact, they were so impressive that he was given “royal privilege” by King Louis XIV. Think of it as the modern patent, but more prestigous back then.

He contributed much to the field of physics, besides being a mathematician. He created the all famous …

$\textbf{Pascal’s Law:}$ states that when there is an increase in pressure at any point in a confined fluid, there is an equal increase at every other point in the container. So basically you use the relation, $\frac{F_1}{A_1} = \frac{F_2}{A_2}$

It’s much easier with a picture. If you look down below…

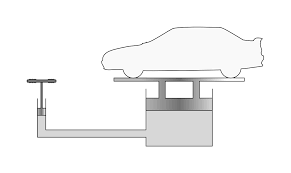
Basically a small force on a small surface area would be able to lift a big car on a big surface area through the property of ratios. Due to his early contribution to the barometer, he had the unit, the Pascal (unit for pressure) named after him. Very cool! He had many more inventions but this article would take an hour to read if I included them all.

In the same year, at thirty years old, he created Pascal’s triangle, a conveinent tabular representation of the binomial coefficents, and one of the most useful tools in probablity.

Major Math Theorems

$\textbf{Pascal’s Theorem:}$

In simple terms, it can be used to prove the collinearity of three intersections among six points in a circle. The image from Brilliant, explains this quite simply.

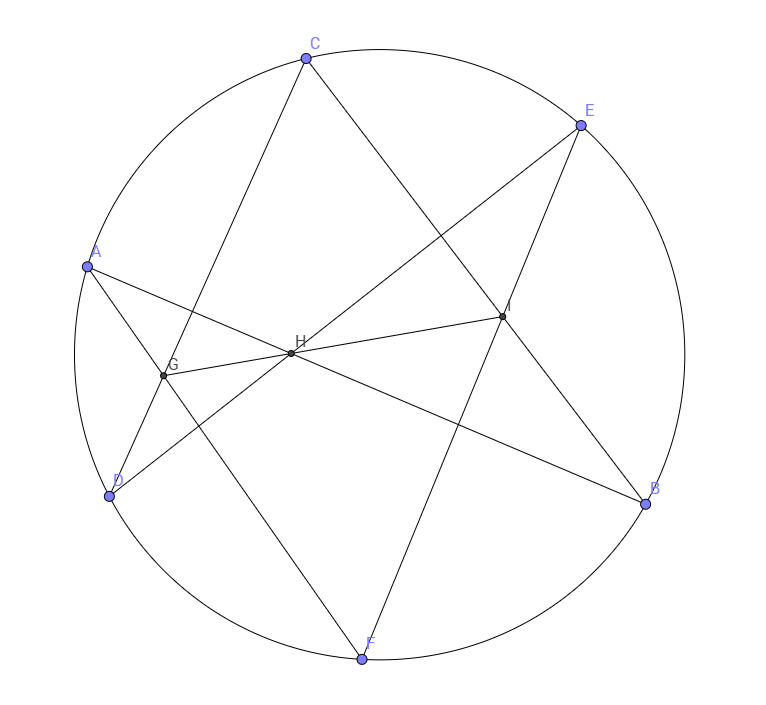
Pascal’s Theorem just states that for any 6 points that are in the circle, then we have the intersections of AB and DE, AF and CD, and BC and EF are all collinear. It’s quite useful in Olympiad math!

$\textbf{Pascal’s Triangle:}$

This is Pascal's Triangle.

The triangle is created by adding the two numbers above it to get a new number. For example, 1 + 1 = 2, 1 + 2 = 3, and so on. This is a triangle that you have certaintly seen before and maybe have had to memorize a couple of the rows here. Where does it actually apply?

Well, the most simplest explanation is that if you have $(x+1)^3$, that’s $x^3 + 3x^2 + 3x + 1$. The coefficents match up to the 3rd row of the triangle. Similarly, for any $(x+1)^n$, the coefficents will follow the nth row of the triangle.

Although, I said that this would appear in probability as well. If I change the numbers of the triangle to look a little different we get…

This is Pascal's Triangle, but rewrittern with binomial coefficents.

While it may look different, the numbers exactly match up with the coefficent. Look down below for a quick crash course on binomial coefficents…

Now, many theorems come about from Pascal’s triangle. For example, the way that a triangle is perpetuated because you two consecutive numbers to get a new one below. This is $\binom{n}{k} + \binom{n}{k-1} = \binom{n+1}{k}$ which is useful for math competitions! There are a gazillion others that I won’t go into, but visit AOPS or Brilliant if you are interested in looking at those!

Final Moments

This is an interesting little tidbit, but when Pascal was 23 years old, his father slipped on a carpet amd broke his hip (possibly fatal). Somehow, this caused him to have a religous revelation. Apparently, this was enough to convince him to switch from Roman Catholicism to Christianity, and some think that Pascal thought his whole family was cursed. So he thought switching his religion might help and he proceeded to live a ascetic from then on.

Going in a full circle, his illness when he was younger came back in a new form at the ripe age of 36. He first got slightly sick, but refused all the doctors because of his philosphy that “Sickness is the natural state of Christians.”

This is Blaise Pascal's Death Mask at 39 years old: a cast taken over the corpse.

Later when his sister died, Jacqeuline, he was incredibly devastated because she was with him through thick and thin. So this caused him to go a little insane. In 1662, Pascal’s health incredibly worsened and he was mostly bed ridden, and now he kinda realized that he should probably go to a hospital. Although, the hospital thought that he was too mentally insane to be in a hospital. He was moved to Paris during this time, and he was experiencing major convulsions and shocks, but still no one except small time doctors would help him. He died on August 19, 1662 and his parting words were “May God Never Abandon Me.”

An autopsy after his death showed that he suffered from brain lesions, grave problems with his stomach and other organs, tuberculosis, stomach cancer, etc. This time the old woman couldn’t go and help him, but he left Earth as a great scientist.